Really, really understanding the area of a triangle (Part 1)

We all learnt this one at school - recite with me : "The area of a triangle is half base times the height", and then the teacher wrote on the board: 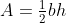 and then the students practiced endless boring substitutions, triangle after triangle after triangle.

But how many of our students really understand what is happening? What is the height? Where does the half come from? Why are we multiplying by a half - aren't we dividing by two? And what's with that strange  obtuse triangle?

Observe how these diagrams are almost monochrome
making it all that harder to explain the ideas.

After spending several weeks with Year 8 and Year 11 classes exploring the challenges of teaching and understanding area of the triangles, it's become very clear to me that many students are going all the way through high school without ever really 'getting it' - which is a pity because the idea is so wonderfully powerful and actually quite simple when you strip away the ornamentation.

Here are the lessons my students taught me about being a better teacher of triangle geometry:

Understanding the key idea is easy - for right triangles and acute triangles

So long as your students are happy with the formula for the area of a rectangle, the logic of the "half the base times the height" formula is stunning clear:

The 'wow' noises that came from the class showed the power of these diagrams! Even better if you have a dynamic geometry tool like GeoGebra. It's just so clear the area of the triangle is half the area of the bounding rectangle. 

That's so obtuse!?!

The hard part came when we looked at obtuse triangles. I am deeply ashamed to confess my bag of tricks was empty at this stage and I had to resort to saying: "Well, the formula works the same for obtuse triangles - trust me!" (blush).  Demonstrating this result using a dynamic geometry drawing tool, comparing the bounding rectangle area to the triangle area didn't quite cut it.

Extra work is needed to understand the diagrams

Many of my students really struggled with the height markings on the obtuse triangle. I think in part because I was initially using monochrome diagrams, and in part because the idea of the 'height' of triangle (as opposed to the length of the sides) wasn't clear.  Here is what I'm going to do next time I first show this diagram ...

Many students don't understand what that dotted line is all about.
Replacing it with a ruler, and explaining the idea of triangle height
 better helped understanding.

Extra work is needed to explore the idea of the 'height' of a triangle

... and at the same time as showing the diagram, we need to reinforce thinking about the difference between the length of something and its height above the ground. Here's what seemed to work: I started by standing tall,  asking how high my head was, and then I leaned over - was my head still as high? No. Then I made a triangle using a school desk as my base, and a stick (a long ruler) as one side of my triangle. I put the ruler vertically on the desk, so it was clear the height = length of the ruler. Then I leaned the ruler over at an angle and asked what the height was now? Some wonderful students jumped up, grabbed another ruler to measure the height. Another look at the diagram of the obtuse triangle with the height marked, and more 'Aha' light bulbs going off!  Next time I'm going to use a loop of string wrapped around the desk to make my dynamic triangle.

Don't assume students are comfortable with the standard formula

I made the mistake of assuming students would be happy with 'half base times height' expressed as 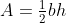 . I was wrong! I heard several students asking - "Why are you multiplying by a half? Why not multiply base times height and divide by two?". And another "Huh? Doesn't multiplying make something bigger?".  For the time being, I'm letting students write 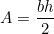or even  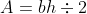. We'll save that story for another day!

And the obtuse triangle?
So is there are easy way to show how an obtuse triangle fits into half the base times height? It turns out there is!  Here's a hint:

Another way to explore triangle area - turn it into a parallelogram. So powerful it works for obtuse triangles too! Image: Wikipedia Triangles article, by Herbee

The idea is so powerful, I'm now seriously thinking we are teaching area of shapes in the wrong order. But that's for Part 2.

With many thanks to my Year 8 students who felt safe and secure enough to ask every possible question - and more - they had about area, triangles, multiplication and algebraic expressions.