Magic Expanding Chelonian - Day 3

Here is a compilation of images over the 3 days. The scale was preserved by using the Day 0 chelonian as a reference.  So the question: How valid was the claim it would grow 600%?  Do I need to go back to the $2 shop and demand my money back? Keen to see what my Year 9 maths class makes of this one....

Click for a full size image

Actually - they won't be getting this ready-to-go picture - that's way too easy. Instead they will be offered 4 raw photos of each day, each picture with a Day 0 turtle for scale reference, as well as access to some real-life expanded chelonians if they want to try some hands-on physical measurements.  If this activity works, I might go out and buy another 15 chelonians.

Magic Expanding Chelonian - Day 1

This magic expanding chelonian is turning out to be even more fun than I expected.... although it is kind of sad what a math teacher does for kicks on Saturday night...

Download GeoGebra file 

I'm guessing the promised 600% growth in 72 hours will be by area - or maybe even by volume. I'm getting scared ....

Am I being too negative (about you-know-what)?

Some days will be rainy days.

So am I being too negative in my recent posts about what I believe are some of the barriers to using laptops in mathematics classrooms?  Some responses to recent feedback. Please feel encouraged to contradict (or support) by posting a comment!

I'm an unashamed enthusiast about laptops. I'm thrilled to have students with laptops in my classroom - along with my Interactive Whiteboard and my HoverCam we can go many places which would be much harder to do without them. I can't imagine not having the technology - and I'm frustrated on a daily basis that my Year 7 and Year 8 students don't have laptops. But what about teachers who aren't so keen on the laptops?

An honest appraisal of what is happening is a prerequisite to understanding and to encouraging change. I really don't think this is being negative. Mathematics teachers have reasons for not using the laptops - they are motivated by concern for the best learning outcomes for their students. I'm not saying I agree with those reasons, but I respect and understand these views. In many of my interviews with teachers not using the laptops, they shared their strong sense of hurt and feelings of being ridiculed or ignored by their technology-enthusiast colleagues.  I suggest we need to work with those concerns - and not avoid discussing them.

About the evidence:

• Where is the evidence for lower use in mathematics classrooms? See the references in the earlier post - they are the major longitudinal studies done in the US. They are conducted by researchers with an active interest and long term commitment to studying 1:1 programs, some of whom have been involved in technology and education study for decades - and typically with a positive disposition to the programs. Their evidence is credible.
• Isn't that old evidence? Yes and no. These reports were published between 2005 and 2010 - and most likely this data was already a year old when published, however, they do reflect findings after many years of 1:1 laptop programs in the USA. In my personal experience, I do see laptop usage increasing over time - I see it in my own faculty - so we can hope there is greater use being made of these new resources.
• Aren't we different in Australia? Yes and no. We do have a lot more support in our 1:1 programs, with major funding for professional development, great technical support and a vast array of teacher support resources. The challenge is not the funding - the challenge is engaging a time-poor and typically conservative profession to participate in the change.
• "But you only looked at a few schools". Absolutely - I was an honours student with a research budget of $0. I make no claim to a representative sample or exhaustive research. All I can say is: "Do  my findings suggest credible reasons why we have lower levels of use of the laptops in mathematics classrooms? Are they consistent with existing research on 1:1 laptop, with mathematics teacher responses to curriculum and technology change?"  There is a wide body of evidence, beyond the studies of 1:1 programs, about mathematics teacher beliefs in their response to technology and curriculum change. In considering our response to mathematics curriculum change, the work of Michael Cavanaugh (2006) is particularly interesting. For recent comprehensive longitudinal research on mathematics teacher beliefs in relation to technology, see the work by Australian researchers Goos and Bennison (2007, 2008) and Pierce and Ball (2009).
• What I'm not saying in my research: I make no claims my work can be generalised to all schools:  my sample is too small, the duration of the work too short, the methodology too limited. I make no claims on laptop usage or teacher beliefs for other school subjects - I haven't read or studied any of this material. And I make no claim about outcomes or the value of 1:1 laptop programs.
• Why pay attention to this exploratory research? It may offer some insights into the reasons behind the previously established lower levels of laptop use by mathematics teachers in their classrooms - and may help us consider what to do about it. There is something different about mathematics when it comes to 1:1 laptops - and the question needs answering. I argue some key beliefs unique to mathematics education in combination with some specific mathematics teaching practices create a strong barrier to widespread adoption of the laptops.
• "In my faculty we use the laptops all the time with all our classes". Yes - there are mathematics faculties where full use of the laptops is being made, where teachers are actively collaborating and supporting each other. We need to get their stories out into the wider mathematics teaching community - told by maths teachers to other maths teachers. And remember : many of the teachers not using the laptops with their students aren't online. Talk to some maths teachers who are not in your online network, who are not in your faculty (if your faculty is one of those actively collaborating on using the laptops) - ask them the questions: What does a student need to do to learn maths? Which  classes will most benefit from exploration activities? Which classes will get most benefit from using the laptops? I think you may be surprised - as I was.
• Won't discussing barriers to laptop usage pander to those who don't want the laptops? People hostile to laptops don't need me to justify their reasons - they have more than enough arguments already. And they probably aren't reading my blog :-) Indeed, it's unlikely you are reading this blog if you are strongly skeptical about using technology for mathematics learning.

So - what can we do? Talk to our mathematics teacher colleagues about the things that concern them - not us.  Better yet - don't talk - show.  Show ways in which laptops can and are successfully used with lower achieving students. Show how laptop use can be integrated into current pen-and-paper practices. Just today I read a great post about getting students to keep a learning journal while doing online learning. Small changes and practical ideas like this can make a big difference in encouraging teachers to try out the technology.

Last word goes to a more experienced and no doubt wiser colleague @Deborah_morton. How do we present the message?  Deborah Morton suggests there are three key elements needed in a presenter of ideas trying to encourage change:  inspiration, trust in the presenter and evidence it works. We can do this!

Do you have a story about using the laptops in a mathematics classroomm you would like to share but don't have time to get a blog going to share the it? Happy to give you a guest slot here!

Further reading

Cavanagh, M. (2006). Mathematics teachers and working mathematically: Responses to curriculum change, in  G. Grootenboer, R. Zevenbergen & M. Chinnappan (Eds.), Identities, Cultures and Learning Spaces (Proceedings of the 28th annual conference of the Mathematics Education Research Group of Australasia) Vol 1, pp. 115-122. Melbourne: MERGA.  http://www.merga.net.au/documents/RP102006.pdf

Goos, M., & Bennison, A. (2007). Technology-enriched teaching of secondary mathematics: Factors influencing innovative practice. In J. Watson & K. Beswick (Eds.), Mathematics: Essential Research, Essential Practice — Volume 1, Proceedings of the 30th Annual Conference of the Mathematics Education Research Group of Australasia (pp.315-324).  Wahroonga: MERGA. http://www.merga.net.au/publications/counter.php?pub=pub_conf&id=398

Goos, M., & Bennison, A. (2008). Surveying the technology landscape: Teachers’ use of technology in secondary mathematics Classrooms. Mathematics Education Research Journal, 20,(3), 102-130.

Pierce, R., & Ball, L. (2009). Perceptions that may affect teachers’ intention to use technology in secondary mathematics classes. Educational Studies in Mathematics, (71)3, 299-317

Weston, M.E., & Bain, A. (2010). The end of techno-critique: The naked truth about 1:1 laptop initiatives and educational change. Journal of Technology, Learning and Assessment, 9(6), 5-25. Retrieved Aug 14, 2011 from http://www.jtla.org.

WCYDWT? Magic Expandable Chelonian

What can you do with this?

The Magic Expandable Chelonian : Grows 600%!
(Do not swallow!)

Yes - it's fun AND educational too!

My head is spinning with possibilities!  I'm very curious to see the questions my different maths classes ask. I bought three of these today at the $2 shop - the plan is to show the class the original packet then see what happens. I'm hoping to try out some version of Dan Meyer's WCYDWT rubric and half way through the period bring out some turtles "I expanded earlier". The packaging suggests dramatic growth in 48 and 72 hours - so I'll get some going a few days earlier.

It's fun and educational - or so the packaging claims. To be honest, I don't even mind if it's not educational - I just want to see what happens to the turtle! And what would happen if I did swallow the turtle and then drank a litre of water?

Next in this series: The Magic Expanding Chelonian - Day 1

Why is maths different when it comes to laptops?

Continuing the series on 1:1 laptops in the mathematics classroom. This post may be a little uncomfortable for all of us, but the factors considered come up again and again for all mathematics teachers - even those of us (like myself) who have drunk the Cool-Aid and are eagerly looking for ways to enrich our teaching through use of technology. In later posts we shall consider the wonderful and amazing things mathematics teachers can  do with laptops - but first we need consider some of the barriers.

In the previous post, we looked at what for many people is an unexpected finding: mathematics teachers have their students use laptops much less than teachers in other subjects. Some reports put this figure at 50% less than other subjects.  When all other factors are taken into account - access to technology, training, confidence, skills - we still find a reluctance to use the 1:1 laptops in the mathematics classroom. And so we ask: Why do maths teachers make these decisions? Is there something different about mathematics?

My research has led me to conclude there is indeed something different when it comes to mathematics.

Mathematics teacher beliefs + mathematics teacher practices :
a powerful combination which often acts as a barrier to using technology.

A core set of beliefs about mathematics and mathematics teaching in conjunction with some strongly entrenched mathematics teaching practices act together as a powerful barrier to widespread use of the laptops in mathematics classrooms.  I see the three key themes at work:

• "Maths is something you do on paper"
• "Laptops aren't suitable for low achieving students"
• "The teacher leads, the student follows"

I make no explicit comment on the validity or otherwise of these commonly held mathematics teacher beliefs and teaching practices - but there is no getting around their effect on 1:1 laptop programs.

"Maths is something you do on paper"

When you ask mathematics teachers what 'real' maths is, and how you 'really' learn it - pen and paper, and I really mean pen and paper the physical media - eventually emerge as a key requirement. Software may be fine to demonstrate and maybe explore mathematics (for some mathematics teachers)- but it's not properly learnt until it's done on paper.

Now consider the very strongly established practice of managing student learning by working in and monitoring output in the student exercise book. Learning outcomes aren't tangible - can't be verified until they are seen in the exercise book.  Entire sequences of classroom practice, homework, outcomes tracking are based on physical movement in and around the student exercise book. You won't find this combination of beliefs and practice in most other subjects. No-one would say you don't understand science, or history, unless you do it on paper. And other subjects are much more receptive to accepting digital learning artifacts as evidence of learning.

Unfortunately there is also a technical hurdle : unlike other subjects, writing in the language of our subject with a computer is hard. It's actually very awkward to write a continual flow of mathematical ideas with standard or even specialised software. 

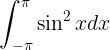
Try writing this   without taking a software detour. Now do twenty lines of it. For now at least, the technology gets in the way of expressing the ideas. While there is powerful and non-intrusive software such as GeoGebra for exploring and demonstrating some parts of mathematics, actually writing long sequences of mathematical language is hard work on the computer.

So: combine the belief that real mathematics is done on paper with a key teaching practice based on writing in exercise books and there isn't much space left for using laptops beyond peripheral extension activities.

"Laptops are not suitable for low achieving students"

We have a real problem in secondary school mathematics: many students are not achieving the learning outcomes. It's no surprise these students don't enjoy maths and are looking for other ways to occupy their time and energy during maths class. Now ask mathematics teachers if using laptops might help make the classroom more engaging, or possibly even provide new ways to help these students with learning mathematics. The answer is a pretty resounding 'no' - there is a widely held belief that laptops are not suitable for low achieving students. Two lines of reasoning are offered: the low achieving students are actually incapable of using the software; and the low achieving students are using the laptops to escape from mathematics and instead engage in off-task behaviour - watching videos, listening to music, playing games. Not like the high achieving students who want to use their laptops for maths.

Some mathematics teachers strongly believe it is in their lower achieving students' best interests to turn off the laptops. These students need to do more maths, and allowing them to use the laptops, which provides more distraction, is actually harming them - teachers motivated by care and compassion for their students make the decision to block use of the laptops. Personally - I don't agree with this approach - indeed I believe the laptops offer us possibilities to re-engage students with mathematics - but this reaction is understandable and consistent with those teachers' beliefs.

Now consider the strongly entrenched teaching practice of  ability streaming, used in mathematics faculties across the country almost without exception, and to a degree not seen in any other school subject. We put the highest achieving students in one class, and then progressively lower achieving students into progressively "lower" class groups, creating entire classes of disengaged, low achieving students.

Combine the belief that low achieving students can't or won't use the laptops for learning with the practice of ability streaming, and we have effectively created entire classrooms where the laptops just will not be used. And indeed this seems to be the case.  Chances are when it comes to secondary mathematics, you will see the laptops being used almost exclusively in the top achieving classes.

"Teacher leads, student follows"

And finally, we consider the strong prevalence in secondary mathematics education of the idea that the teacher should show-and-tell, and that students should follow-and-practice. While it would be an overstatement to say this is always the case, it is the prevalent belief among maths teachers.  A student armed with a laptop can be disruptive to 'teacher leads, students follows' - and although the presence of the laptops doesn't automatically guarantee a change in pedagogy, the benefits of the laptops seem to me to be diminished if they are merely used to automate lead-and-follow practices.  This combo of belief+practice isn't unique to mathematics teaching by any means, but I do think we are more likely to follow traditional teaching and learning approaches than other subjects.

In conclusion ...

So by considering these three powerful belief+practice combinations, which are to a large degree unique to secondary mathematics education, we can begin to see just why laptops are used at up to 50% less than in other subjects. I find that even in my own practice, keen as I am on using technology with my students, I'm often falling into these memes: I do worry about not doing the maths on paper - "is it real maths?", I do worry about exercise books, and I do find myself dismissing using the laptops with my lower achieving students. And I catch myself 'holding the mouse' often.

Am I optimistic about using technology in the mathematics classroom? Absolutely. But I also recognise there are powerful beliefs and practices in our subject domain - and these contribute to making using the laptops harder in mathematics teaching and learning.

This post is high level summary of research I conducted during 2010. The study examined the use of the laptops in mathematics classrooms at five schools, looking at usage levels, how the laptops are used and the role of teacher skill, confidence, knowledge and beliefs factors. The work builds on a body of knowledge as found in nearly 100 published papers on technology in education, mathematics teaching using technology, and mathematics teaching beliefs and practices. An academic paper is currently in preparation.

So what is happening with laptops in maths classrooms?

Continuing the series about 1:1 laptops in mathematics classrooms 

If you ask someone who doesn't sit in a high school maths faculty, they will probably tell you that maths teachers just love using computers. Computers = programming = maths ... doesn't it? You may be surprised to know this is not usually the case - certainly not when it comes to actual teaching practice.

How much has the high school mathematics classroom changed since 1950?
Change the blackboard for a whiteboard - or if you are fortunate, an electronic
 whiteboard (IWB) - but how much has the teaching really changed?

Are students using their laptops in the mathematics classroom? The research findings are clear and unambiguous: when it comes to school 1:1 laptop programs, students are using their laptops in mathematics classrooms much less than other in subjects. Indeed, some of the major studies report usage levels at 50% less compared to other subjects. This picture of significantly lower levels of laptop use in mathematics classrooms is consistent no matter how the data is collected: from classroom observations to questionnaires and interviews with teachers, students and parents. 

Are laptop programs making a difference to mathematics outcomes? While there have been some interesting signals in the data (see references below), the uncomfortable truth is more measured. When we look at the mass of evidence, we do not see a consistent positive effect on mathematics outcomes in standardised tests.  Even the most enthusiastic laptop advocates who initially reported strong results on standardised tests (Silvernail is the most prominent) have become more cautious and now look to other measures to evaluate 1:1 programs. However before we dismiss the laptops, we do need to consider more carefully: Are we measuring the right outcomes? Are we measuring maths classrooms that are actually using the laptops? Are we looking at how the laptops are being used?   But there is no avoiding the lack of strong evidence after ten years of 1:1 programs - we just can't claim the mere presence of the technology will radically boost maths test results. It's that old "education silver bullet" story all over again. If you still haven't read it, read "The Naked Truth" article. Seriously, you will be glad you did :-), whether you think 1:1 programs are helpful or a distraction.

Sometimes looking at the "average" hides important details:  My own research at five secondary schools shows that, at the schools I visited, the overall use of laptops in mathematics classrooms is indeed quite low. But more interesting was  the wide variation in the use of laptops - some mathematics teachers use the laptops much more than other mathematics teachers.  I found three very different and distinct groups of teachers in terms of how frequently their students used the laptops:

So immediately we see the more general, more aggregated data may mask interesting subtleties in what's happening with 1:1 programs. If we want to see what is really going on, we need to look more carefully how individual teachers and their classrooms are responding to 1:1 programs.

But the fact remains: mathematics teachers aren't using the laptops as much as teachers in other subjects.

Which really has us wondering: 

And that's the real focus of my research. While many research papers have reported laptop use in mathematics classrooms is noticeably less than in other subjects - no-one seems to have asked: "Why aren't mathematics teachers making more use of the laptops?"

And that's going to be the subject of the next few posts in this series. It turns out there is indeed "something different about mathematics".


Background information

One-to-one laptop programs: the essential ingredients

Continuing this series of posts about using laptops in the mathematics classroom, we go back to basics and look at the essential elements of what makes a one-to-one laptop program.

So what makes a one-to-one laptop program?

Three key elements are the hallmarks of a one-to-one program:

1. Each student has their own computing device - and it's portable.
   It's this ratio of one-device-per-student that gives us the name one-to-one (1:1). I say 'computing device' because the technology changes fast - usually we mean a laptop, but there are variations. Will the iPad or some other tablet device be the new device? Possibly - although we want students creating content not just consuming it - so it seems to me they are going to need a good input device - a stylus or a keyboard.  From a teacher's perspective, 1:1 means they can assume every student in their class has a computing device ready to work on (or most of them). No need to book the school computer labs in advance - assuming they are available - or move the class to another room. Don't underestimate how painful, time-consuming and annoying this can be for a busy teacher on a tightly scheduled program - enough to put you off using the computer labs all together.
   
   
2. The students are connected to the internet - usually via WiFi.
   Connected to the internet means students are connected to external social and knowledge networks. Students and teachers also have options to create and participate in social and knowledge networks specific to their learning activities. Two immediate flow on effects: the teacher is no longer the source of all knowledge - the network has arrived into the classroom - and a whole new range of possibilities for collaborative learning are now available.
   
   
3. Students can take their computing device home Learning with digital tools and being connected to social and knowledge networks can continue at home - the student has their own device and does not need to compete for computing and network access with other family members. Many of my students tell me that when their parents or their elder siblings come home, they take over the family computer. And for some students, their school issued laptop is the only computer in the house.

It's easy to under-estimate the potential impact on the teaching and learning environment resulting from of each of these elements. However as we consider 1:1 programs, there is something we must never forget ..

Arguably, the most essential ingredient of a 1:1 program is the pedagogy.

There is no silver bullet.  Giving laptops to students and leaving it at that will not make a difference. It's what students and teachers do with them that may make a difference.  As Bebell and O'Dwyer (2010) remind us - in most high profile programs, how we use the laptops, how we learn with them, is often not the key focus. Much research looks at implementation and outcomes, with little focus on what is done with the laptops. Most program evaluations take a black-box approach: put laptops into the system, come back one, two, four years later and take measurements to see if standardised test results have improved. While this is a perfectly valid approach, it doesn't necessarily tell us that much about what teachers and students are doing with the laptops, or how to get the most value from the programs.

If this is a topic that interests you (the effect of technology on learning outcomes), stop reading this post now and read this incredible paper by Weston & Bain (2010):

Weston & Bain (2010)
IMHO, the most insightful article written on the subject in the last
ten years - and I've read at least a hundred papers on the subject for my
thesis. It is an opinion piece, but draws heavily on quality research.

"The Naked Truth" is a well reasoned, rational and articulate summary of current one-to-one research which then goes on to ask the 'why' and 'how' questions, in the context of a century of 'education reform' programs. Whether you are skeptic or fanboy when it comes to technology in the classroom, you will find this article challenging reading. So am I skeptic or a fanboy? A bit of both - let's say a fanboy with skeptical eye.

In the next post in the series, I will look at what the research says about 1:1 programs in relation to mathematics classroom. You may be surprised...

References:
Bebell, D., & O’Dwyer, L.M. (2010). Educational outcomes and research from 1:1 computing settings. Journal of Technology, Learning, and Assessment, 9(1), 5-26.

Weston, M.E., & Bain, A. (2010). The end of techno-critique: The naked truth about 1:1 laptop initiatives and educational change. Journal of Technology, Learning and Assessment, 9(6), 5-25. Retrieved Aug 14, 2011 from http://www.jtla.org.

"So are you on Facebook, sir?"

Student: "So are you on Facebook, sir?"

Mr Zuber: (incredulous look) "Of course I am!" (do you think I'm a total loser?)

Student: (impressed at Mr Zuber's coolness) : "Oh wow! Can I be your friend?"

Mr Zuber: (incredulous look) "Why would you want to be a friends with a teacher?"

Student: "But I want to see who all your friends are!"

Mr Zuber: "But they are all maths teachers!"

Student: "Hmm.. yeah .. maybe not...."

I've found this approach works wonders dissuading students asking the perennial Facebook question and beats having to explain teachers can't and shouldn't do that - which they knew before they asked the question anyway :-)

Powerful learning with GeoGebra - but who is holding the mouse?

This is the second of two short reflections on using (or not using) laptops in my maths teaching.

In the last few weeks I have had the pleasure of tutoring a bright young student, let's call him Paul*, who needed just a little extra help with some of the more advanced parts of the Year 10 math syllabus. Heading out to my first session with Paul, I instinctively brought my trusty Asus EeePC ready to fire up GeoGebra. I say instinctively because I just can't imagine doing any sort of advanced mathematics without GeoGebra around - even just for my own purposes. GeoGebra is just part of my kit.

And sure enough, within minutes, Paul and I were exploring the ideas from his course textbook using GeoGebra - what does the parabola look like when when we change parameters? Concepts that Paul had missed previously came to him faster than I could demonstrate them - he saw what was happening in the dynamic graphs even before we discussed them.  But then something even better happened - Paul started asking lots of 'what if' questions - what if we did this to the function, what about that? GeoGebra let us freely and rapidly explore his questions. Later as part of practicing the learning, we played what I call "graph racing games": I wrote down a function like   and gave Paul a few minutes headstart to graph it by hand on paper, and try to get it done (correctly) before I could graph it using GeoGebra. It didn't take long before Paul could do every variation without error.

We moved on to trigonometry, and I asked Paul if he had seen the graphs for sin(x) and cos(x) - he had and we drew them in GeoGebra to be remind ourselves. And then he asked - unprompted - what about tan(x)? He hadn't seen it yet. I was about to show the graph, when a voice from a past teacher of mine said 'Stop!'. I asked Paul what he expected. "Sort of like sin(x), just bigger - maybe it goes from 4 to -4".  We had a look at the graph - Paul nearly fell of his chair:

Even more fun to be had when we moved from solving equations like   to slightly more tricky ones like this

Without GeoGebra we would have just done the problems as an algebraic manipulation - but we did have GeoGebra - so no reason not to take a peek ahead of what is coming in Year 11. Certainly got a reaction ....

This is not what Paul expected to see when solving
an equation rearranged to be a quadratic!

After each surprise, we took time to explore the reason why the graph looked so odd - Paul hadn't seen asymptotes before - and uncovered all sorts of number properties along the way.  I was really thrilled to see how powerful teaching and learning can be when there is a laptop with GeoGebra right there in front of the student.  But there was a problem .....

Who is holding the mouse?

It took me two weeks to realise - but all this time, I was fiercely keeping hold of the mouse. I was driving the application. My own love of the software, the power of the exploration and the idea that I was the teacher was leading me to be the driver of the application.  Perhaps I also wanted to stay focused on the math, and didn't want Paul to get distracted using the software. Finally I let go of the mouse - and let Paul do all the driving. He worked out how to do the basics in a few minutes (seriously!) - and before long, he was investigating his own questions - and even decided to name a theorem after himself.

Paul worked out these two triangles are similar. Knowing this
fact made an entire set of exercises in his textbook trivial.

Seeing how powerful using GeoGebra was, and knowing it's a free application, I suggested Paul install the GeoGebra java app, or even just the WebStart link on his laptop. To my surprise I discovered his school laptop doesn't have Java installed (to stop students playing games), that there is no math software on his laptop, and that in fact, his maths teacher doesn't even allow laptops to be used in their class.

Paul's school managed laptop has no maths software,
and the laptops aren't allowed in maths class.

Fortunately Paul can use GeoGebra at home!

Some take home thoughts:

• Who is holding the mouse? Are you really prepared to let go of the control and allow the student to take the exploration where they want it to go? Will you let them make the mistakes and wrong turns using the software that are so essential to learning?
• When using graphing software - never just show the graph. Stop! Ask first for a prediction. Then see what the graph looks like. And then ask that all important question: Why does it look like that?
• A teacher's personal use of a maths tool makes it much more likely they will use such software with their students.
• Using maths software on the laptops is best when the technology is (almost) transparent - you want the conversation to be on the math, not on the tool. Until the teacher and student have this fluency, using the laptops for math is hard work.
• Just because a school and a student has a laptop - don't assume there is math software on it, and don't be surprised to find the math teacher actively prevents use of the official school laptop in their class.

In the next post in this series, we shall look at the current research on one-to-one laptops and their use in mathematics classrooms. 

* Paul is a pseudonym. My thanks to Paul and his parents for allowing me to share this story.

Demonstrating angle sum of triangle using an IWB

Here is a quick demo of how to show the angle sum of a triangle using an Interactive Whiteboard and SMART Notebook, starting with blank screen. It's surprisingly quick and fun to do - my Year 7 class hooted in delight.

Grab a triangle from the shapes menu.

Use three different colour pens to mark the angles -
can be as messy as you wish!

Group the triangle with the three coloured paint patches
 to make a single object.

Clone the group twice to make three identical triangles.

Grab the second triangle by the rotation handle and start rotating it.

Drag the second triangle to join the first triangle, aligning
so two different coloured angles are adjacent.

Bring in the third triangle, aligning so
the third angle is adjacent to the other two.

The three angles line up to form a straight line = 180 degrees. QED!

My Year 7 class loved this - they half-jokingly suggested I was rigging it - and insisted I try out different triangles and watched very intently to see if I was sneakily stretching or adjusting the triangles.  Enjoy - but don't miss out doing it the traditional way with a paper triangle and cutting off the angles - nothing beats hands on feel for maths.

Next in this series: IWB Tips: Making invisible algebra visible