 |
| With apologies to South Park. |
"Algebra is the offer made by the devil to the mathematician. The devil says: `I will give you this powerful machine, it will answer any question you like. All you need to do is give me your soul: give up geometry and you will have this marvellous machine.’”
Atiyah (2001)
Atiyah (2001)
When I was a young student, while I found Euclidean geometric proofs fascinating (yes - I was a math nerd), the glory of Algebra - the revelation of being able to work with symbols and expressions blinded me to anything else. Perhaps it was because I'm not that spatially aware (as my long suffering World of Warcraft guild mates found out this weekend when I kept running into the fire breathing dragons despite repeated deaths...) - but I just took to algebra like a duck to water. And then I discovered coordinate geometry - who needed shapes anymore? I could turn every geometry problem I met into an algebra problem .. even it if was a bit messy sometimes!
However while relearning mathematics 20(ish) years later as part of my post-graduate teaching degree, I discovered the joy and elegance of the geometric view. So many ideas, including algebraic ideas, are clearer, easier to learn and remember when seen geometrically. As Lockhart points out - how much more interesting is the area of a triangle when seen geometrically as a half rectangle, as opposed to a formula learnt by rote?
Now that I'm teaching maths, I'm exploring what happens when we use geometry to help understand algebra. It was interesting to observe my top Year 9 class when set the task to explain the "difference of squares" using a geometric argument:
I handed out sheets of coloured paper and scissors, but how they resisted! Some drew small sketches of the idea, but just refused to cut out accurate representations and manipulate the shapes. I chuckled at their resistance, because I knew that's what I would have done in my school days - the algebra is 'obvious' - what's the point? We got there in the end - no doubt that will be recorded as one of those 'weird activities' I made them do :-)
Does using a geometric demonstration help learn ideas? Absolutely! I have no difficulty remembering the formula for the sum of angles in a polygon now, because I can see the triangles arranged inside it; I feel the triangle area formula - and now even the odd looking rhombus area formula is in my bones - because I can see the triangles; and the difference of squares - well it's just so clear; and you absolutely know that ^2 \neq a^2 + b^2) because you can see it in the diagram - those two extra bits are in there!
because you can see it in the diagram - those two extra bits are in there!
Michael Atiyah was right when he said that having to choose between algebra and geometry is like asking someone if they would rather be blind or deaf : "On the whole we prefer to have both faculties" (Atiyah, 2001).
Atiyah, M. (2001). Mathematics in the 20th Century: geometry versus algebra, Mathematics Today, 37(2), 46- 53.
Illustrations made in PowerPoint, GeoGebra and Paint. GeoGebra is an important part of the solution to breaking down the false dichotomy between algebra and geometry - a very good reason to use it in class!
Answer to difference of squares problem: Cut the top green rectangle into the two obvious pieces, rotate the narrow green piece to line it up below the larger green piece. The area covered is very clearly 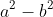



dsada
ReplyDelete